Problem:
A quadrilateral that has consecutive sides of lengths and is inscribed in a circle and also has a circle inscribed in it. The point of tangency of the inscribed circle to the side of length divides that side into segments of lengths and . Find .
Answer Choices:
A.
B.
C.
D.
E.
Solution:
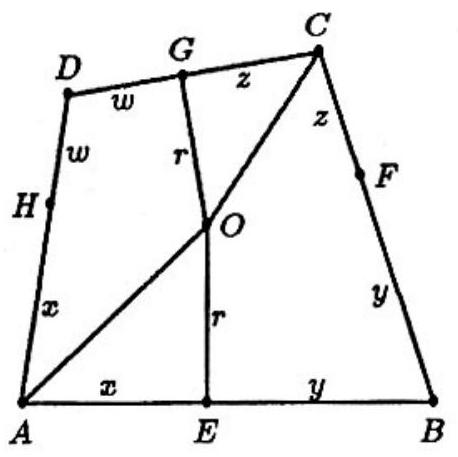
Let the inscribed circle have center and radius . Label the quadrilateral where and . Label the points of tangency with the inscribed circle , and , and let and be the distances from these points of tangency to the vertices of the quadrilateral as indicated in the figure. Since the quadrilateral is inscribed in a circle, is supplementary to . Thus, since bisects and bisects and are complementary. Hence . Thus . Similarly, . Hence , which leads to
Solve and simultaneously for and to obtain .
Note. This quadrilateral has an inscribed circle because . The shape of this quadrilateral is unique since it is inscribed in a circle.