Problem:
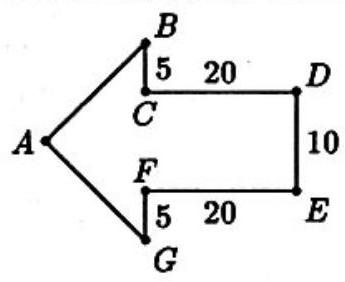
In the arrow-shaped polygon [see figure], the angles at vertices A,C,D,E and F are right angles, BC=FG=5,CD=FE=20, DE=10, and AB=AG. The area of the polygon is closest to
Answer Choices:
A. 288
B. 291
C. 294
D. 297
E. 300
Solution:
Rectangle CDEF has area 10⋅20=200. Triangle ABG is isosceles with base angles 45∘. The altitude to base BG is 10, so the area of the triangle is 21⋅20⋅10=100. Thus the total area of the polygon is 200+100=300.
OR
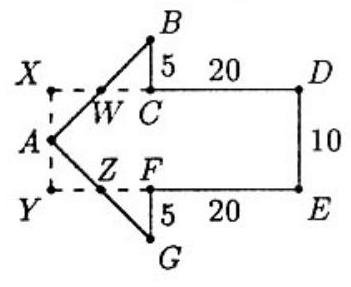
Extend DC to X and EF to Y where X and Y are on the line parallel to DE through A. By symmetry, AX=AY= 21DE=5=BC. If AB intersects DX at W, then △AXW≅△BCW since ∠WAX=∠B=45∘= ∠BWC=∠AWX. Similarly, if AG intersects EY at Z, then △AYZ≅△GFZ. Hence the area of the arrow equals the area of rectangle DXYE which is 10(20+5+5)=300.