Problem:
Point is units from the center of a circle of radius . How many different chords of the circle contain and have integer lengths?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
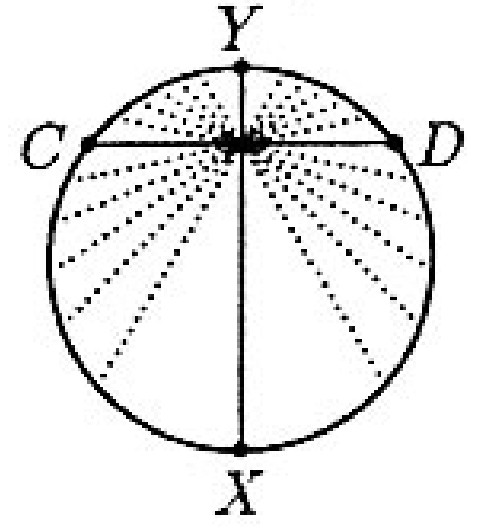
The longest chord through is the diameter, , which has length . The shortest chord through , , is perpendicular to this diameter. Hence its length is . As the chords rotate through point , their lengths will take on all real numbers between and twice. [See figure.] Thus, for each of the five integers strictly between and there are two chords of length through . This gives a total of chords with integer lengths.