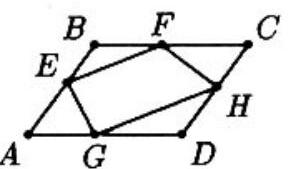
Problem:
Let ABCD be a parallelogram of area 10 with AB=3 and BC=5. Locate E,F and G on segments AB,BC and AD, respectively, with AE=BF= AG=2. Let the line through G parallel to EF intersect CD at H. The area of the quadrilateral EFHG is
Answer Choices:
A. 4
B. 4.5
C. 5
D. 5.5
E. 6
Solution:
The area of polygon P1P2⋯Pn will be denoted by [P1P2⋯Pn]. Since [ABCD]=10 and AD=BC=5, the distance between lines AD and BC is 10/5=2. Thus, if the altitude of △AEG from E is h, then the altitude of △BEF from E is 2−h. Since AG=BF=2,
[AEG]+[BEF]=21AG⋅h+21BF⋅(2−h)=h+(2−h)=2.
Similarly, since the sum of the altitudes of triangles CFH and DGH from H is 2 and CF=DG=3, it follows that [CFH]+[DGH]=3. Hence[0pt]
[ EFHG ]
=[ABCD]−([AEG]+[BEF]+[CFH]+[DGH])=10−(2+3)=5.
OR
Note that ABFG is a parallelogram. Hence [EFG]=21[ABFG], and similarly, [HFG]=21[CDGF]. Consequently, [EFHG]=21[ABCD]=5.
Note. Not only is the choice of E and H completely arbitrary on their respective segments, but F and G can be chosen as any two points on BC and AD as long as BF=AG.
Challenge. As the solution indicates, if a diagonal of a quadrilateral, Q, inscribed in a parallelogram, P, is parallel to a side of P, then the area of Q. is half the area of P. Can you prove the converse?