Problem:
Five equilateral triangles, each with side , are arranged so they are all on the same side of a line containing one side of each. Along this line, the midpoint of the base of one triangle is a vertex of the next. The area of the region of the plane that is covered by the union of the five triangular regions is
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Partition the figure into equilateral triangles as shown. Since each side of each of these triangles has length , the total area is .
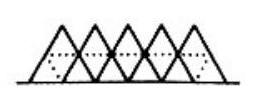
In each of the two equilateral triangles at the ends, insert the segment connecting the midpoints of the outer side and the side on the line, as indicated. Observe that the area covered is enclosed by congruent rhombi and congruent equilateral triangles. The rhombi have diagonals with lengths and , while the triangles have sides . Hence the area is
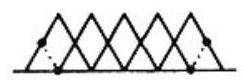
Note. There are a number of other ways to compute the area. For example: compute the area of the five large triangles and subtract the area of the four small triangles of overlap; or compute the area of the smallest trapezoid which contains the figure and subtract the area of the four small missing triangles