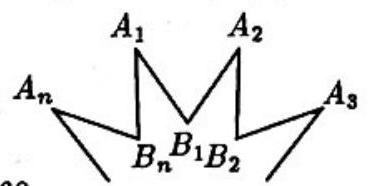Problem:
Part of an " n-pointed regular star" is shown. It is a simple closed polygon in which all 2n edges are congruent, angles A1,A2, …,An are congruent and angles B1,B2,…,Bn are congruent. If the acute angle at A1 is 10∘ less than the acute angle at B1, then n=
Answer Choices:
A. 12
B. 18
C. 24
D. 36
E. 60
Solution:
Partition the n-pointed regular star into the regular n-gon B1B2⋯Bn and n triangles congruent to △B1A2B2, and note that the sum of the star's interior angles is
(n−2)180∘+n180∘=(2n−2)180∘.
Since the interior angles of the star consist of n angles congruent to A1 and n angles congruent to 360∘−B1,
(2n−2)180∘=n∠A1+n(360∘−∠B1), or n(∠B1−∠A1)=2⋅180∘.
Since ∠B1−∠A1=10∘,n=36.
Note. In general, the sum of the interior angles of any N-sided simple closed polygon, convex or not, is (N−2)180∘.