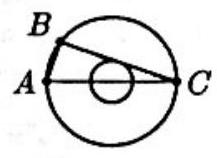
Problem:
The ratio of the radii of two concentric circles is . If is a diameter of the larger circle, is a chord of the larger circle that is tangent to the smaller circle, and , then the radius of the larger circle is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Draw the radius from the center of the circles to the point where is tangent to the smaller circle. Since , and are similar right triangles, so
Thus the radius, , of the smaller circle is since . Hence the radius of the larger circle is since the ratio of the radii is .
.jpg)