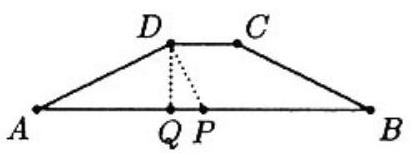
Problem:
Let ABCD be an isosceles trapezoid with bases AB=92 and CD=19. Suppose AD=BC=x and a circle with center on AB is tangent to segments AD and BC. If m is the smallest possible value of x, then m2=
Answer Choices:
A. 1369
B. 1679
C. 1748
D. 2109
E. 8825
Solution:
Since ABCD is isosceles, the center of the circle, P, must be the midpoint of AB. When x=m, the circle must be tangent to AD at D and to BC at C. (Why?) Let Q be the foot of the perpendicular from D to AB. Then △ADP is a right triangle with hypotenuse AP, and DQ is its altitude to the hypotenuse. Since △ADQ∼△APD,
APAD=ADAQ, so m2=AD2=AQ⋅AP=273⋅292=1679.