Problem:
Let be the set of points on the rays forming the sides of a angle, and let be a fixed point inside the angle on the angle bisector. Consider all distinct equilateral triangles with and in . (Points and may be on the same ray, and switching the names of and does not create a distinct triangle.) There are
.jpg)
Answer Choices:
A. exactly such triangles.
B. exactly such triangles.
C. exactly such triangles.
D. exactly such triangles.
E. more than such triangles.
Solution:
The figure shows the original configuration with the vertex of the angle labeled and three line segments drawn from to . Point is chosen so that . Thus is equilateral. Point is any point on segment , and is on the other side of with . Since , and , we have . Thus, , and hence . Since and is also equilateral. Since was an arbitrary point on segment , it follows that there are an infinite number of the required equilateral triangles.
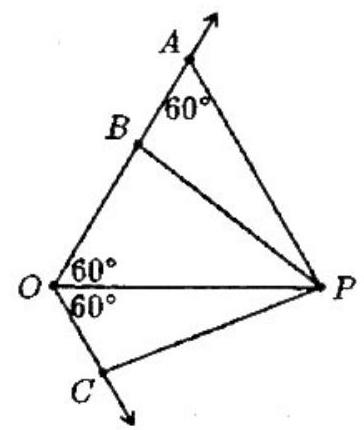
Let be the vertex of the angle, choose on the one ray so and choose any point on segment . Consider on the other ray with . Then is a cyclic quadrilateral since angles and are supplementary. The arc of the circumscribed circle is subtended by both and , so
Since is equiangular and therefore equilateral. Since the point on segment was arbitrary, there are an infinite number of equilateral triangles .
Query. If the rays form a different angle, would there still be an infinite number of equilateral triangles?