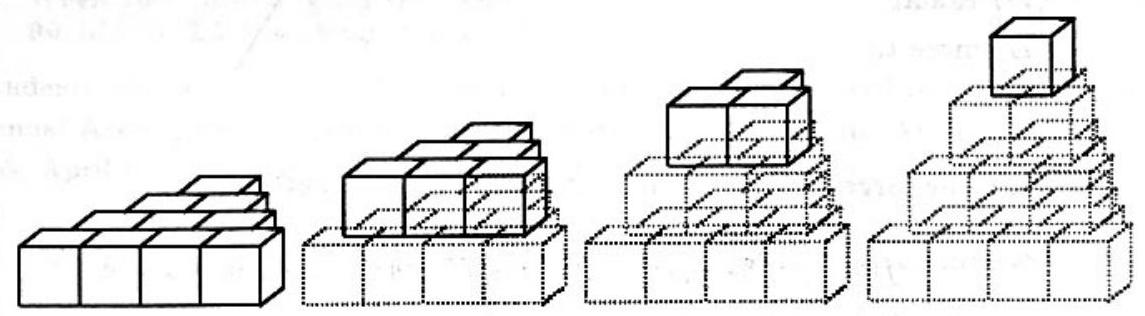
Problem:
Twenty cubical blocks are arranged as shown. First, 10 are arranged in a triangular pattern; then a layer of 6, arranged in a triangular pattern, is centered on the 10; then a layer of 3, arranged in a triangular pattern, is centered on the 6; and finally one block is centered on top of the third layer. The blocks in the bottom layer are numbered 1 through 10 in some order. Each block in layers 2,3 and 4 is assigned the number which is the sum of the numbers assigned to the three blocks on which it rests. Find the smallest possible number which could be assigned to the top block.
Answer Choices:
A. 55
B. 83
C. 114
D. 137
E. 144
Solution:
Intuitively, we note that the center cube in the first layer is counted most often and should be assigned the number 1 and those in the corners are used least and should be assigned 8,9, and 10. For example, to arrive at the correct answer, assign the numbers to the bottom layer in this pattern:
97268135410
More formally, suppose the assignment of the numbers to the bottom layer is:
v2e3e1e5v1ce2e6e4v3
The arrangement of numbers in the second layer is:
(e3+e5+v2)(c+e1+e3)(e1+e2+v1)(c+e5+e6)(c+e2+e4)(e4+e6+v3)
The arrangement of numbers in the third layer is
(2c+e1+2e3+2e5+e6+v2)(2c+2e1+2e2+e3+e4+v1)(2c+e2+2e4+e5+2e6+v3)
So t=6c+3(e1+e2+e3+e4+e5+e6)+(v1+v2+v3) is the number assigned to the top block. Thus, the value of t is minimized when c=1,{e1,e2,…,e6}= {2,3,…,7} and {v1,v2,v3}={8,9,10}. Hence, the minimum value of t is 6(1)+3(2+3+⋯+7)+(8+9+10)=114.