Problem:
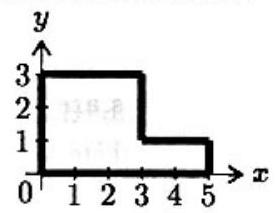
In the -plane, consider the -shaped region bounded by horizontal and vertical segments with vertices at , and . The slope of the line through the origin that divides the area of this region exactly in half is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
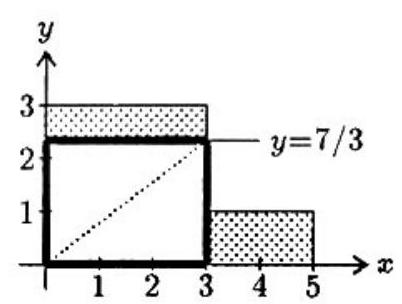
The area of the region is . Label the vertices as indicated in the figure. Since the area of trapezoid is and the area of triangle is , it follows that the desired line, , intersects the line at some point , where . The area of the trapezoid above the line is
which equals when .
.jpg)
The area to the right of the line in the L-shaped region is . Since , the area above the line is also . The diagonal of the rectangle which remains when these two rectangles of area are discarded is the line which bisects the area of the -shaped region. This diagonal connects the origin with and has slope .