Problem:
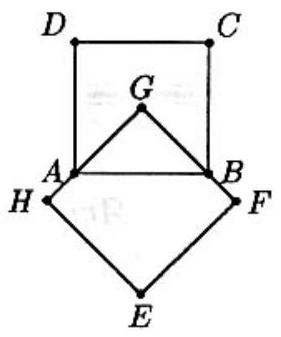
Squares and are congruent, , and is the center of square . The area of the region in the plane covered by these squares is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Each square has side , and so has area . The overlap, , has area one-fourth that of square . Thus, the area covered is .
Since is an isosceles right triangle with hypotenuse , it follows that the length of each of its legs is so its area is . Each square has area . Thus, the total area covered is .
Note. It is not necessary that and coincide with the diagonals of square . The area of the overlap is constant as long as is the center of .
.jpg)