Problem:
In triangle . If there is a point strictly between and such that , then
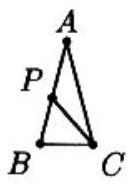
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Let . Then since . By the exterior angle theorem, . Since , it follows that . Thus since . Therefore, , or .
.jpg)
Problem:
In triangle . If there is a point strictly between and such that , then
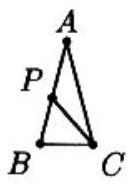
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Let . Then since . By the exterior angle theorem, . Since , it follows that . Thus since . Therefore, , or .
.jpg)