Problem:
Triangle ABC is inscribed in a circle, and ∠B=∠C=4∠A. If B and C are adjacent vertices of a regular polygon of n sides inscribed in this circle, then n=
Answer Choices:
A. 5
B. 7
C. 9
D. 15
E. 18
Solution:
Since 180∘=∠A+∠B+∠C=∠A+4∠A+4∠A, it follows that ∠A=20∘. Therefore, BC=2∠A=40∘, which is 1/9 of 360∘. Thus the polygon has 9 sides.
OR
If ∠C is partitioned into four angles congruent to ∠A, the four chords associated with the arcs subtended by these angles will be congruent to BC. These four chords plus four obtained analogously from ∠B, together with BC, form the n=9 sides of the inscribed regular polygon.
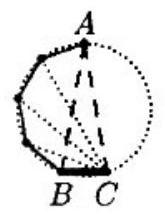
Note. In general, if ∠B=∠C=k∠A, then n=2k+1.
.jpg)
