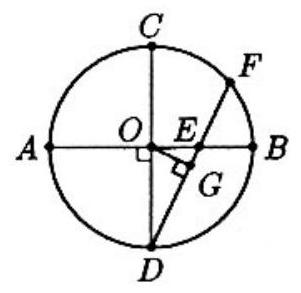
Problem:
In the figure, AB and CD are diameters of the circle with center O, AB⊥CD, and chord DˉFˉ intersects AB at E. If DE=6 and EF=2, then the area of the circle is
Answer Choices:
A. 23π
B. 247π
C. 24π
D. 249π
E. 25π
Solution:
Draw segment FC. Angle CFD is a right angle since arc CFD is a semicircle. Then right triangles DOE and DFC are similar, so
DFDO=DCDE.
Let DO=r and DC=2r. Substituting, we have
8r=2r6,2r2=48,r2=24
Then the area of the circle is πr2=24π.
OR
Let OA=OB=r and OE=x. Substituting into AE⋅EB=DE⋅EF gives (r+x)(r−x)=6⋅2 so In right triangle EOD, r2−x2=12. r2+x2=36.
Add to find 2r2=48. Thus, the area of the circle is πr2=24π.
OR
Construct OG⊥DF with G on DF. Then DG= 21DF=4. Since OG is an altitude to the hypotenuse of right triangle EOD, we have DODE=DGDO. Let DO=r. Then r6=4r, so r2=24, and the area of the circle is πr2=24π.
.jpg)