Problem:
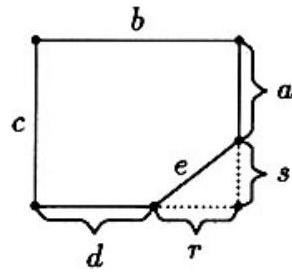
A pentagon is formed by cutting a triangular corner from a rectangular piece of paper. The five sides of the pentagon have lengths and , although this is not necessarily their order around the pentagon. The area of the pentagon is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Let the sides of the pentagon be and , and let and be the legs of the triangular region cut off as shown. The equation has no solution in positive integers when or . Therefore, equals or , and the possibilities for are the well-known Pythagorean triples
Since and do not appear among any of the pairwise differences of , the only possibility is . Then , and .
Hence, the area of the pentagon is .