Problem:
A large cube is formed by stacking unit cubes. A plane is perpendicular to one of the internal diagonals of the large cube and bisects that diagonal. The number of unit cubes that the plane intersects is
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Suppose the coordinates of the vertices of the unit cubes occur at for all . The equation of the plane that bisects the large cube's diagonal from to is . That plane meets a unit cube if and only if the ends of the unit cube's diagonal from to lie on opposite sides of the plane. Therefore, this problem is equivalent to counting the number of the triples with for which . Only of these triples do not satisfy these inequalities:
Therefore, of the unit cubes are intersected by the plane.
A sketch can help you visualize the unit cubes intersected by the plane. Suppose the plane is perpendicular to the interior diagonal at its midpoint. That plane intersects the surface of the large cube in a regular hexagon.
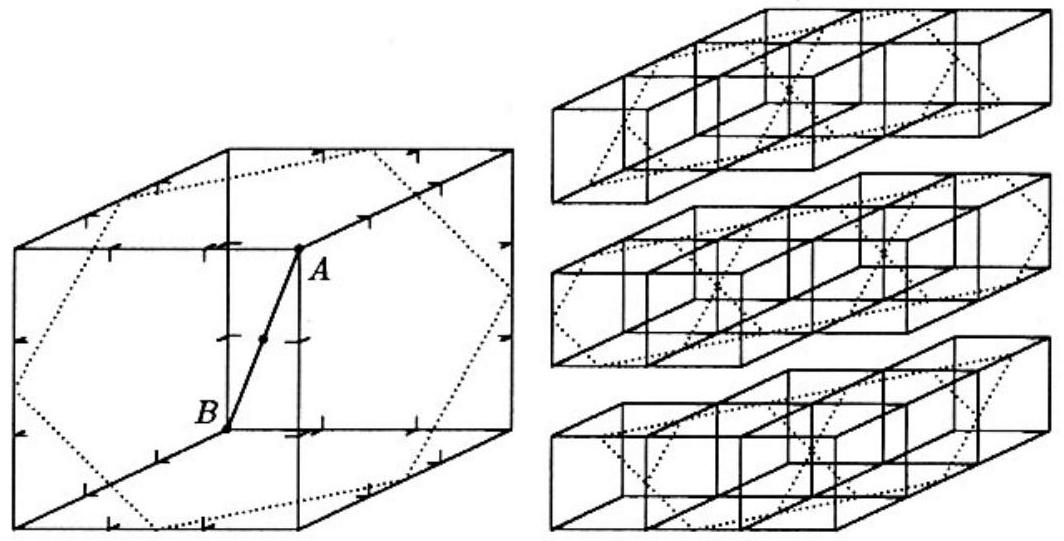
The sketch shows that nineteen of the twenty-seven unit cubes are intersected by this plane, with six each in the bottom and top layers and seven in the middle layer. The corner unit cube at vertex and the three unit cubes adjacent to it are missed by this plane, as are the four symmetric to these at vertex .