Problem:
Given a circle of radius , there are many line segments of length that are tangent to the circle at their midpoints. Find the area of the region consisting of all such line segments.
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The endpoints of each of these line segments are at distance from the center of the circle. The region is therefore an annulus with inner radius and outer radius . The area covered is .
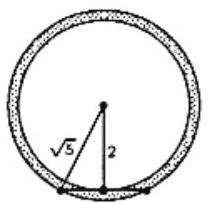
Note. The area of the annular region covered by the segments of length does not depend on the radius of the circle.