Problem:
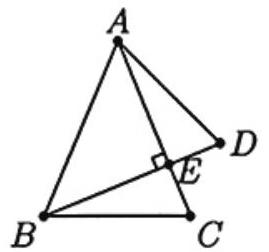
Triangles ABC and ABD are isosceles with AB= AC=BD, and BD intersects AC at E. If BD⊥AC, then ∠C+∠D is
Answer Choices:
A. 115∘
B. 120∘
C. 130∘
D. 135∘
E. not uniquely determined
Solution:
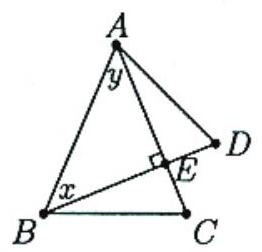
Let ∠ABD=x and ∠BAC=y. Since the triangles ABC and ABD are isosceles, ∠C=(180∘−y)/2 and ∠D=(180∘−x)/2. Then, noting that x+y=90∘, we have
∠C+∠D=(360∘−(x+y))/2=135∘.
OR
Consider the interior angles of pentagon ADECB. Since triangles ABC and ABD are isosceles, ∠C=∠B and ∠D=∠A. Since BD⊥AC, the interior angle at E measures 270∘. Since 540∘ is the sum of the interior angles of any pentagon,
∠A+∠B+∠C+∠D+∠E=2∠C+2∠D+270∘=540∘,
from which it follows that ∠C+∠D=135∘.
.jpg)