Problem:
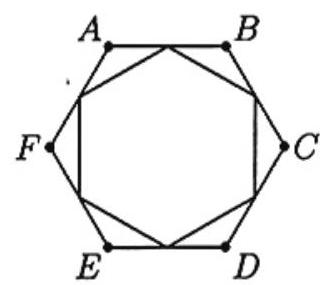
The midpoints of the sides of a regular hexagon are joined to form a smaller hexagon. What fraction of the area of is enclosed by the smaller hexagon?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
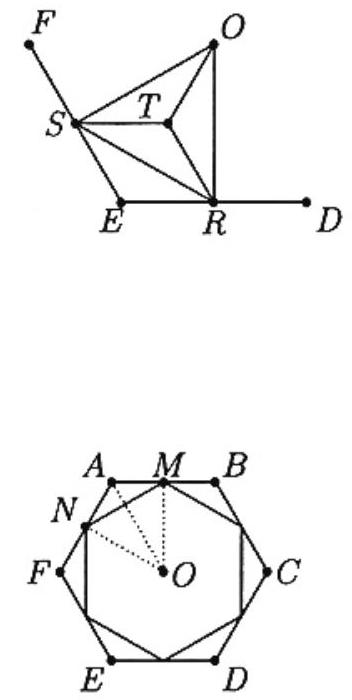
Let and be the vertices of the smaller hexagon adjacent to vertex of the larger hexagon, and let be the center of the hexagons. Then, since , quadrilateral encloses of the area of , encloses of the area of the smaller hexagon, and is equilateral. Let be the center of . Then triangles , and are congruent isosceles triangles with largest angle . Triangle is an isosceles triangle with largest angle and a side in common with , so is partitioned into four congruent triangles, exactly three of which form . Since the ratio of the area enclosed by the small regular hexagon to the area of is the same as the ratio of the area enclosed by to the area enclosed by , the ratio is .
Let and denote the midpoints of and , respectively. Then since is a triangle and . It follows that the hexagons are similar, with similarity ratio . Thus the desired quotient is .