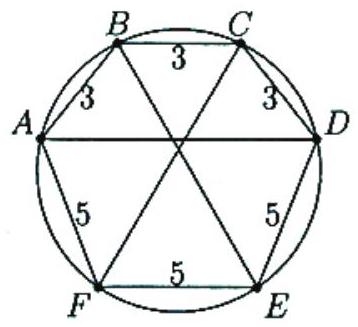
Problem:
A hexagon inscribed in a circle has three consecutive sides each of length 3 and three consecutive sides each of length 5. The chord of the circle that divides the hexagon into two trapezoids, one with three sides each of length 3 and the other with three sides each of length 5, has length equal to m/n, where m and n are relatively prime positive integers. Find m+n.
Answer Choices:
A. 306
B. 349
C. 369
D. 389
E. 409
Solution:
In hexagon ABCDEF, let AB=BC=CD=3 and let DE=EF= FA=5. Since arc BAF is one third of the circumference of the circle, it follows that ∠BCF=∠BEF=60∘. Similarly, ∠CBE=∠CFE=60∘. Let P be the intersection of BE and CF,Q that of BE and AD, and R that of CF and AD. Triangles EFP and BCP are equilateral, and by symmetry, triangle PQR is isosceles and thus also equilateral. Furthermore, ∠BAD and ∠BED subtend the same arc, as do ∠ABE and ∠ADE. Hence triangles ABQ and EDQ are similar. Therefore,
EQAQ=DQBQ=EDAB=53.
It follows that
PQ+52AD−PQ=53 and 2AD+PQ3−PQ=53.
Solving the two equations simultaneously yields AD=360/49, so m+n=409.
OR
In hexagon ABCDEF, let AB=BC=CD=a and let DE=EF=FA= b. Let O denote the center of the circle, and let r denote the radius. Since the arc BAF is one-third of the circle, it follows that ∠BAF=∠FOB=120∘. By using the Law of Cosines to compute BF two ways, we have a2+ab+b2=3r2. Let ∠AOB=2θ. Then a=2rsinθ, and
AD=2rsin(3θ)=2rsinθ⋅(3−4sin2θ)=a(3−r2a2)=3a(1−a2+ab+b2a2)=a2+ab+b23ab(a+b).
Substituting a=3 and b=5, we get AD=360/49, so m+n=409.
OR
In hexagon ABCDEF, let AB=BC=CD=3 and minor arcs AB,BC, and CD each be x∘, let DE=EF=FA=5 and minor arcs DE,EF, and FA each be y∘. Then
3x∘+3y∘=360∘, so x∘+y∘=120∘.
Therefore, ∠BAF=120∘, so BF2=32+52−2⋅3⋅5cos120∘=49 by the Law of Cosines, so BF=7. Similarly, CE=7. Using Ptolemy's Theorem in quadrilateral BCEF, we have
BE⋅CF=CF2=15+49=64 so CF=8.
Using Ptolemy's Theorem in quadrilateral ABCF, we find AC=39/7. Finally, using Ptolemy's Theorem in quadrilateral ABCD, we have AC2= 3(AD)+9 and, since AC=39/7, we have AD=360/49 and m+n=409.
Note. Ptolemy's Theorem: If a quadrilateral is inscribed in a circle, the product of the diagonals equals the sum of the products of the opposite sides.