Problem:
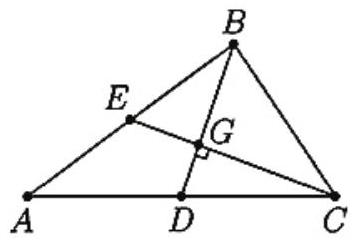
Medians and of triangle are perpendicular, , and . The area of triangle is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Let the medians meet at . Then and the area of triangle is . Since is a median, triangles and have the same area. Hence the area of the triangle is .
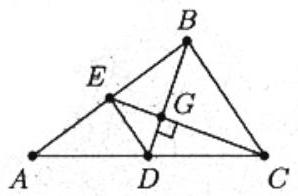
Since the medians are perpendicular, the area of the quadrilateral is half the product of the diagonals . (Why?) However, and are midpoints, which makes the area of triangle one fourth of the area of triangle . Thus the area of is three fourths of the area of triangle . It follows that the area of triangle is .