Problem:
A circle with center is tangent to the coordinate axes and to the hypotenuse of the triangle as shown, where . To the nearest hundredth, what is the radius of the circle?
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Let and denote the points of tangency on the - and -axes, respectively, and let be tangent to the circle at . Tangents to a circle from a point are equal, so and . Let and . Because , the radius of the circle is
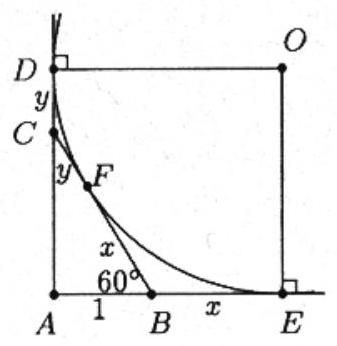
Let be the radius of the circle. The area of square , may also be expressed as the sum of the areas of quadrilaterals and and triangle . This is given by , where . Thus
Solving for using the quadratic formula yields the positive solution
Note. The circle in question is called an escribed circle of the triangle .