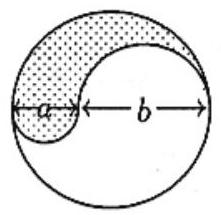
Problem: a a b b
Answer Choices:
A. a b b a
B. a b b a
C. a 2 b 2 b 2 a 2
D. a + b 2 b 2 b a + b
E. a 2 + 2 a b b 2 + 2 a b b 2 + 2 a b a 2 + 2 a b
Solution:
The area of the shaded region is
π 2 ( ( a + b 2 ) 2 + ( a 2 ) 2 − ( b 2 ) 2 ) = π 2 a + b 2 ( a + b 2 + a − b 2 ) = π ( a + b ) a 4 2 π ( ( 2 a + b ) 2 + ( 2 a ) 2 − ( 2 b ) 2 ) = 2 π 2 a + b ( 2 a + b + 2 a − b ) = 4 π ( a + b ) a
and the area of the unshaded region is
π 2 ( ( a + b 2 ) 2 − ( a 2 ) 2 + ( b 2 ) 2 ) = π 2 a + b 2 ( a + b 2 + b − a 2 ) = π ( a + b ) b 4 2 π ( ( 2 a + b ) 2 − ( 2 a ) 2 + ( 2 b ) 2 ) = 2 π 2 a + b ( 2 a + b + 2 b − a ) = 4 π ( a + b ) b
Their ratio is a / b a / b