Problem:
Three non-overlapping regular plane polygons, at least two of which are congruent, all have sides of length . The polygons meet at a point in such a way that the sum of the three interior angles at is . Thus the three polygons form a new polygon with as an interior point. What is the largest possible perimeter that this polygon can have?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
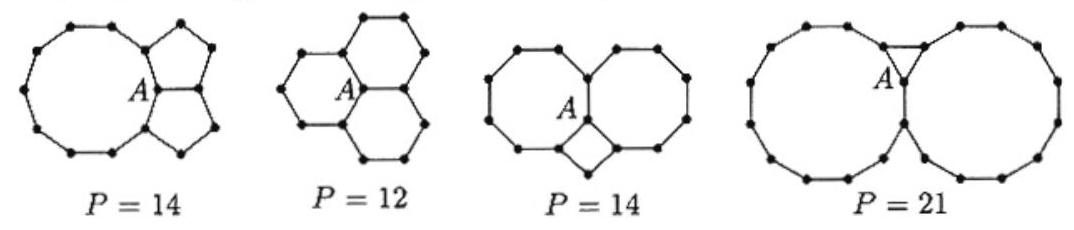
The interior angle of a regular -gon is . Let be the number of sides of the congruent polygons and let be the number of sides of the third polygon (which could be congruent to the first two polygons). Then
Clearing denominators and factoring yields the equation
whose four positive integral solutions are , and . These four solutions give rise to polygons with perimeters of and , respectively, so the largest possible perimeter is .