Problem:
A tetrahedron with four equilateral triangular faces has a sphere inscribed within it and a sphere circumscribed about it. For each of the four faces, there is a sphere tangent externally to the face at its center and to the circumscribed sphere. A point is selected at random inside the circumscribed sphere. The probability that lies inside one of the five small spheres is closest to
Answer Choices:
A.
B.
C.
D.
E.
Solution:
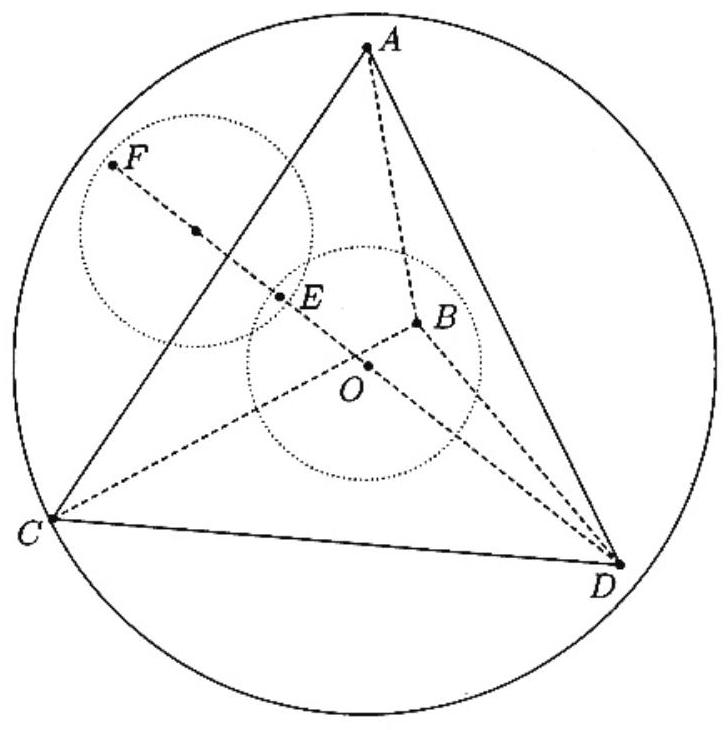
Let , and be the vertices of the tetrahedron. Let be the center of both the inscribed and circumscribed spheres. Let the inscribed sphere be tangent to the face at the point , and let its volume be . Note that the radius of the inscribed sphere is and the radius of the circumscribed sphere is . Draw , and to obtain four congruent tetrahedra , and , each with volume that of the original tetrahedron. Because the two tetrahedra and share the same base, , the ratio of the distance from to face to the distance from to face is ; that is, . Thus the volume of the circumscribed sphere is . Extend to meet the circumscribed sphere at . Then . Thus , so the sphere with diameter is congruent to the inscribed sphere, and thus has volume . Similarly, each of the other three spheres between the tetrahedron and the circumscribed sphere have volume . The five congruent small spheres have no volume in common and lie entirely inside the circumscribed sphere, so the ratio is the probability that a point in the circumscribed sphere also lies in one of the small spheres. The fraction is closer to than it is to any of the other choices.