Problem:
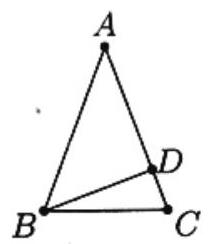
Consider all triangles satisfying the following conditions: is a point on for which and are integers, and . Among all such triangles, the smallest possible value of is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Let and . By the Pythagorean Theorem, . Hence , which yields . Since and are positive integers, the only possibilities are and . The second of these gives the least possible value of , namely .