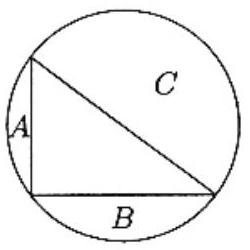
Problem:
A circle is circumscribed about a triangle with sides 20,21, and 29, thus dividing the interior of the circle into four regions. Let A,B, and C be the areas of the non-triangular regions, with C being the largest. Then
Answer Choices:
A. A+B=C
B. A+B+210=C
C. A2+B2=C2
D. 20A+21B=29C
E. A21+B21=C21
Solution:
Since 202+212=292, the converse of the Pythagorean Theorem applies, so the triangle has a right angle. Thus its hypotenuse is a diameter of the circle, so the region with area C is a semicircle and is congruent to the semicircle formed by the other three regions. The area of the triangle is 210, hence A+B+210=C. To see that the other options are incorrect, note that
(A) A+B<A+B+210=C;
(C) A2+B2<(A+B)2<(A+B+210)2=C2;
(D) 20A+21B<29A+29B<29(A+B+210)=29C; and
(E) A21+B21>A21>C21.