Problem:
What is the largest number of acute angles that a convex hexagon can have?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The sum of the angles in a convex hexagon is and each angle must be less than . If four of the angles are acute, then their sum would be less than , and therefore at least one of the two remaining angles would be greater than , a contradiction. Thus there can be at most three acute angles. The hexagon shown has three acute angles, , and .
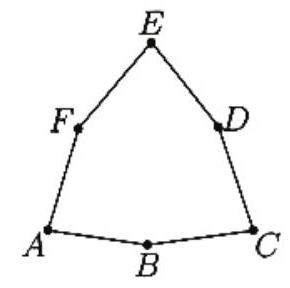
The result holds for any convex -gon. The sum of the exterior angles of a convex -gon is . Hence at most three of these angles can be obtuse, for otherwise the sum would exceed . Thus the largest number of acute angles in any convex -gon is three.