Problem:
Given a point on a triangular piece of paper , consider the creases that are formed in the paper when , and are folded onto . Let us call a fold point of if these creases, which number three unless is one of the vertices, do not intersect. Suppose that , and . Then the area of the set of all fold points of can be written in the form , where , and are positive integers and is not divisible by the square of any prime. What is
Solution:
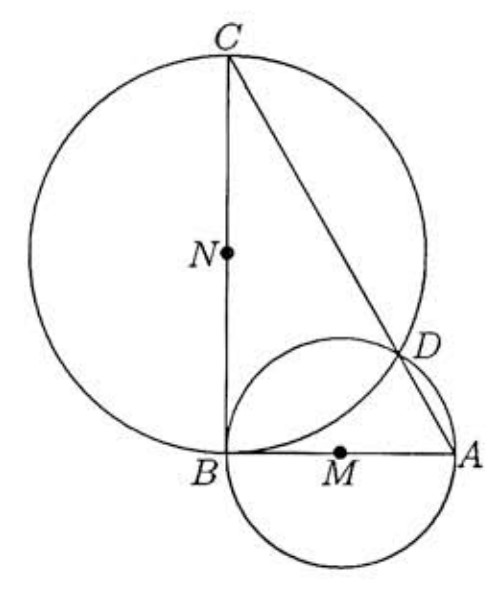
We claim that the set of all fold points of is the region common to the interiors of the circles that have and as their diameters. To establish this, first show that the creases formed by folding vertices and onto are disjoint if and only if lies inside the circle that has as diameter. To see this, note that the crease formed by folding any point onto is part of the perpendicular bisector of . If is outside the circle with diameter , then is not obtuse, for is acute, and angles and are at most and respectively. Therefore the circumcenter of is inside the triangle, requiring that the creases intersect. On the other hand, if is inside the circle that has diameter , then the perpendicular bisectors of and meet at a point that is separated from by , so the creases do not meet inside . If is on the circle, then the creases meet on . A similar discussion applies to the circle that has as diameter and to the circle that has as diameter. Note, however, that all interior points of are inside the latter circle. Thus the set of fold points of the triangle is the region common to the interior of the triangle and the interiors of the two circles with diameters and .
These two circles both intersect at , the foot of the perpendicular from to . The region in question is therefore bounded by two circular arcs. One is a arc of radius , centered at , the midpoint of ; the other is a arc of radius , centered at , the midpoint of . The areas of triangles and are and , respectively. The areas of sectors and are and , respectively. The area that we seek is the sum of the sectors' areas minus the sum of the triangles' areas, which simplifies to . The desired sum is .
The problems on this page are the property of the MAA's American Mathematics Competitions