Problem:
A function f is defined on the complex numbers by f(z)=(a+bi)z, where a and b are positive numbers. This function has the property that the image of each point in the complex plane is equidistant from that point and the origin. Given that ∣a+bi∣=8 and that b2=m/n, where m and n are relatively prime positive integers, find m+n.
Solution:
Because (a+bi)z is equidistant from z and 0,∣(a+bi)z−z∣=∣(a+bi)z∣. Thus ∣a−1+bi∣=∣a+bi∣, or (a−1)2+b2=a2+b2, so a=21. Now use the information ∣a+bi∣=8 to deduce that b2=64−41=4255, so that m+n=259.
OR
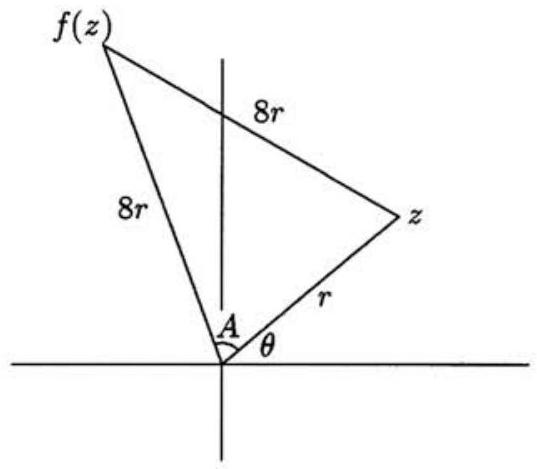
Let z=rcisθ=r(cosθ+isinθ), where r is positive and 0≤θ<2π, and let a+bi=8cisA, where 0<A<π/2. Thus f(z)=8rcis(θ+A). Notice that cosA=8rr/2=161, because the triangle in the figure is isosceles. It follows that
b2=82sin2A=64(1−cos2A)=4255.
Thus m+n=259.
The problems on this page are the property of the MAA's American Mathematics Competitions