Problem:
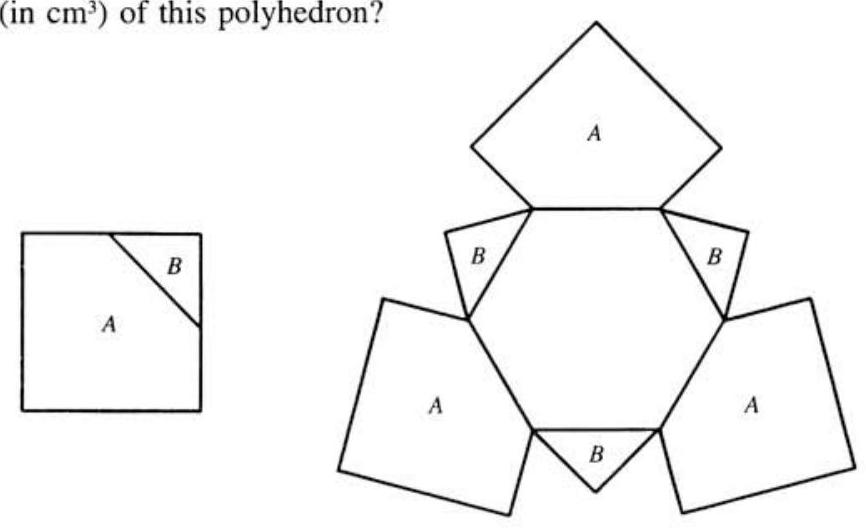
Three squares are each cut into two pieces and , as shown in the first figure below, by joining the midpoints of two adjacent sides. These six pieces are then attached to a regular hexagon, as shown in the second figure, so as to fold into a polyhedron. What is the volume in ) of this polyhedron?
Solution:
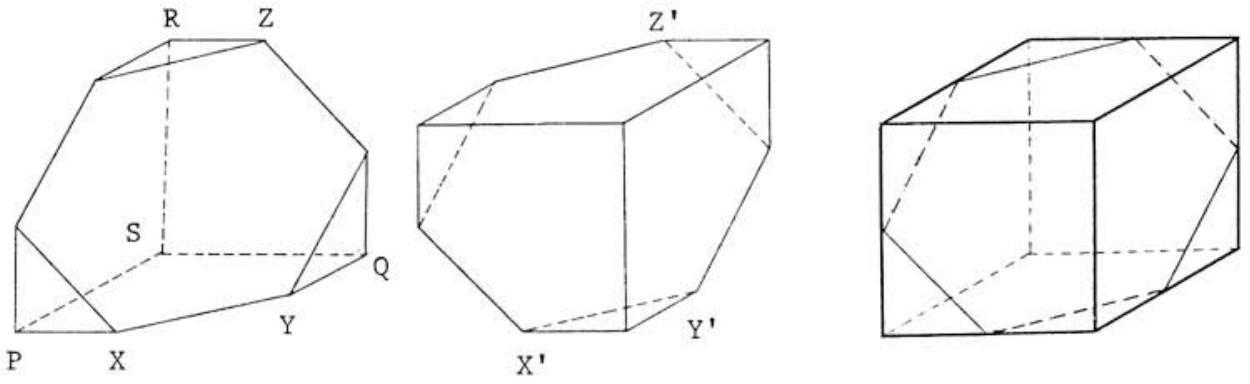
At each of the vertices and , marked in the first figure below, each of the three facial angles measures . Consequently, the polyhedron may be immediately recognized as a portion of a cube. Moreover, two such polyhedra may be fitted together along their hexagonal faces. To accomplish this, flip and rotate by the second polyhedron (as shown in the second figure below), and then slide them together until and and , as wel1 as and coincide. As shown in the third figure below, the result of the procedure is a cube of volume or . Therefore, the volume of the polyhedron under consideration is or .
The problems on this page are the property of the MAA's American Mathematics Competitions