Problem:
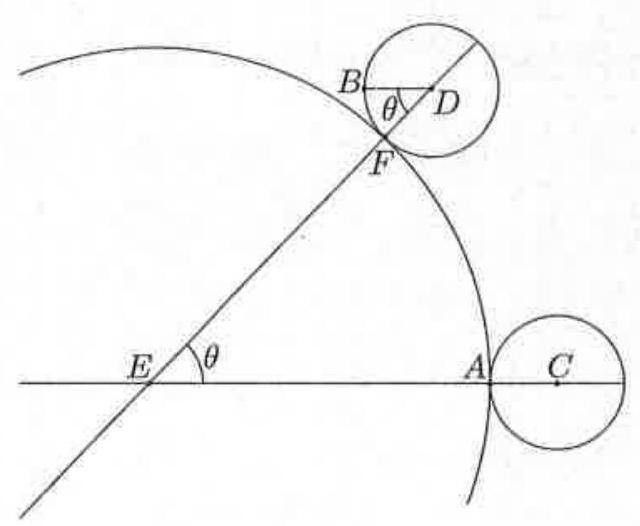
A disk with radius is externally tangent to a disk with radius . Let be the point where the disks are tangent, be the center of the smaller disk, and be the center of the larger disk. While the larger disk remains fixed, the smaller disk is allowed to roll along the outside of the larger disk until the smaller disk has turned through an angle of . That is, if the center of the smaller disk has moved to the point , and the point on the smaller disk that began at has now moved to point , then is parallel to . Then , where and are relatively prime positive integers. Find .
Solution:
Let be the point on the circumference of the larger disk where the smaller disk is tangent after it has rolled through . Let . Because line is parallel to line is also . The arc along the larger disk from to is the same length as the arc on the smaller disk whose central angle is the reflex . That central angle is therefore , and implying . The Law of Cosines applied to shows that . The distance from to line is . Thus . The requested sum is .
The problems on this page are the property of the MAA's American Mathematics Competitions