Problem:
The solid shown has a square base of side length . The upper edge is parallel to the base and has length . All other edges have length . Given that , what is the volume of the solid?
.jpg)
Solution:
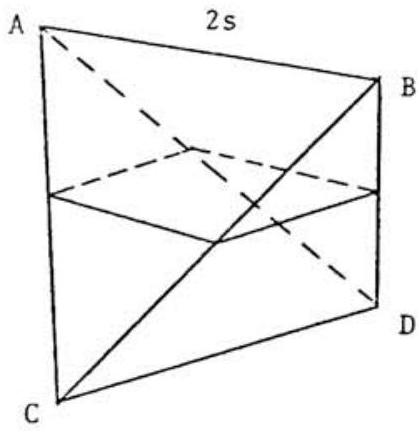
Consider the regular tetrahedron , shown on the next page, that has edge length . Connect the midpoints of and . The quadrilateral thus determined is a square (why?) and the plane of this square divides the tetrahedron into two solids that are identical with the solid given in the problem. Thus, we have only to find the volume of the tetrahedron and then divide by .
The formula for the volume of a regular tetrahedron of side length - its derivation requires only right-triangle trigonometry - is
Thus, substituting and taking gives .
The problems on this page are the property of the MAA's American Mathematics Competitions