Problem:
The adjoining figure shows two intersecting chords in a circle, with on minor arc . Suppose that the radius of the circle is 5 , that , and that is bisected by . Suppose further that is the only chord starting at which is bisected by . It follows that the sine of the central angle of minor arc is a rational number. If this number is expressed as a fraction in lowest terms, what is the product
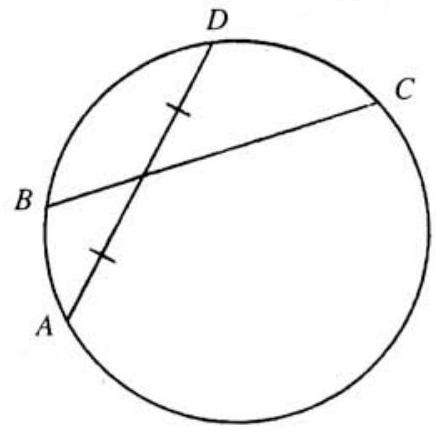
Solution:
Consider the family of all chords emanating from . Then the locus of the endpoints of these chords is the given circle of radius and the locus of their midpoints is an internally tangent circle (at ) of radius . (We have simply shrunk the given circle relative to by a factor of .) Now must be tangent to the smaller circle. For if it cut that circle twice, as in Figure , then there would be two chords emanating from that are bisected by .
.jpg)
.jpg)
Next consider Figure , where and are the centers of the two circles and is tangent to the smaller circle (at ) as described before. We introduce the following construction lines: (through ), , and . We seek . We will find this by first finding all three sides of . We have
- and :
- .
- is a rectangle, so and .
- is a right triangle with and , so .
- so .
- is a right triangle, so .
We now have all three sides of , so by the Law of Cosines applied to we obtain
Thus and the desired answer is .
The problems on this page are the property of the MAA's American Mathematics Competitions