Problem:
Consider the paper triangle whose vertices are , and .The vertices of its midpoint triangle are the midpoints of its sides. A triangular pyramid is formed by folding the triangle along the sides of its midpoint triangle.What is the volume of this pyramid?
Solution:
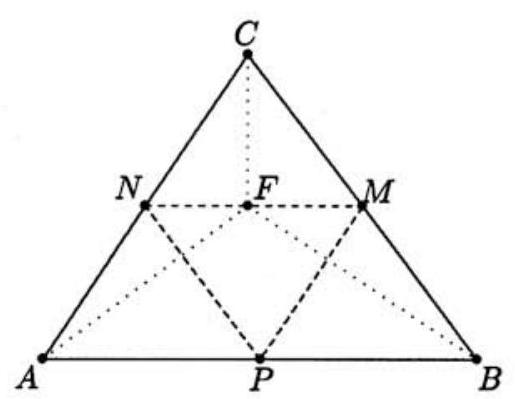
Assign coordinate triples to the vertices, so that , and midpoints , and . Without loss of generality, assume that triangle remains fixed when triangle is folded. Vertex must then stay in the plane (which is perpendicular to midline ), vertex must stay in the plane (which is perpendicular to midline ), and vertex must stay in the plane
(which is perpendicular to midline ). The intersection of these three planes includes , which happens to be on . The planes also intersect at , the fourth vertex of the pyramid. Notice that . Because the planes are all perpendicular to triangle , the altitude drawn to the base of pyramid is . The volume of the pyramid is therefore
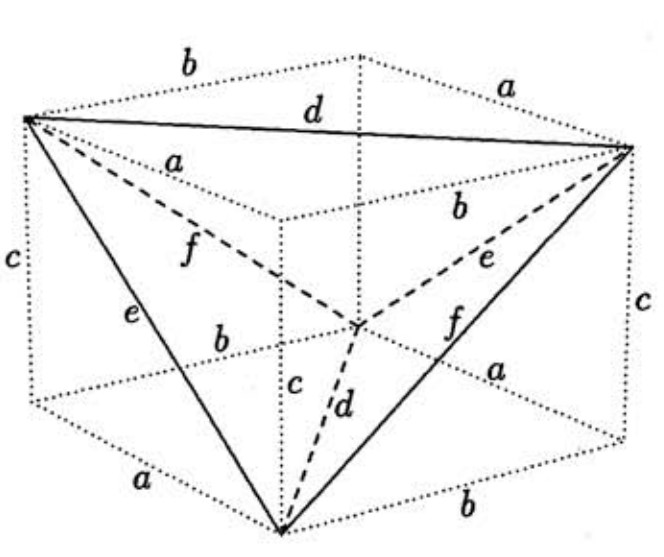
The pyramid is a tetrahedron with four congruent acute faces. Hence its edges may be regarded as diagonals of the faces of a rectangular parallelepiped, as shown below. The edges are , and . The edges of the parallelepiped are , and , where , and . Solve these equations simultaneously to find that , and . The parallelepiped consists of four congruent pyramids, each of volume , as well as the given pyramid. Thus the volume of the given pyramid is .
The problems on this page are the property of the MAA's American Mathematics Competitions