Problem:
A function f is defined for all real numbers and satisfies
f(2+x)=f(2−x) and f(7+x)=f(7−x)
for all real x. If x=0 is a root of f(x)=0, what is the least number of roots f(x)=0 must have in the interval −1000≤x≤1000?
Solution:
First we use the given equations to find various numbers in the domain to which f assigns the same values. We find that
f(x)=f(2+(x−2))=f(2−(x−2))=f(4−x)(1)
and that
f(4−x)=f(7−(x+3))=f(7+(x+3))=f(x+10)(2)
From Equations (1) and (2) it follows that
f(x+10)=f(x)(3)
Replacing x by x+10 and then by x−10 in Equation (3), we get f(x+10)=f(x+20) and f(x−10)=f(x). Continuing in this way, it follows that
f(x+10n)=f(x), for n=±1,±2,±3,…,(4)
Since f(0)=0, Equation (4) implies that
f(±10)=f(±20)=⋯=f(±1000)=0,
necessitating a total of 201 roots for the equation f(x)=0 in the closed interval [−1000,1000].
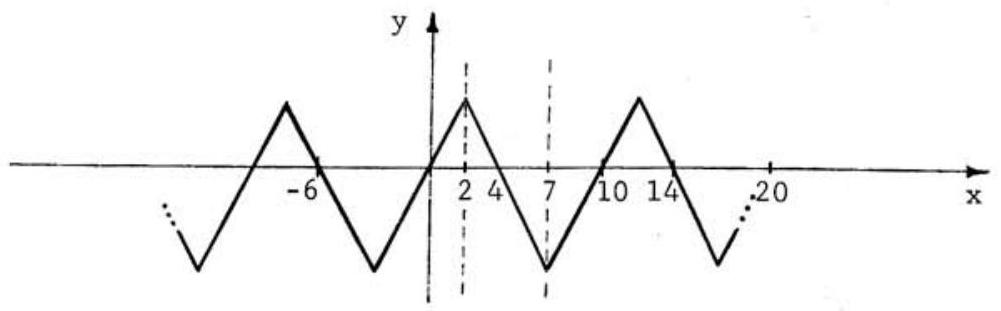
Next note that by setting x=0 in Equation (1), f(4)=f(0)=0 follows. Therefore, setting x=4 in Equation (4), we obtain 200 more roots for f(x)=0 at x=−996,−986,…,−6,4,14,…,994. Since the zig-zag function pictured below satisfies the given conditions and has precisely these and no other roots, the answer to the problem is 401.
The problems on this page are the property of the MAA's American Mathematics Competitions