Problem:
Equilateral triangle is inscribed in circle , which has radius . Circle with radius is internally tangent to circle at one vertex of . Circles and , both with radius , are internally tangent to circle at the other two vertices of . Circles , and are all externally tangent to circle , which has radius , where and are relatively prime positive integers. Find .
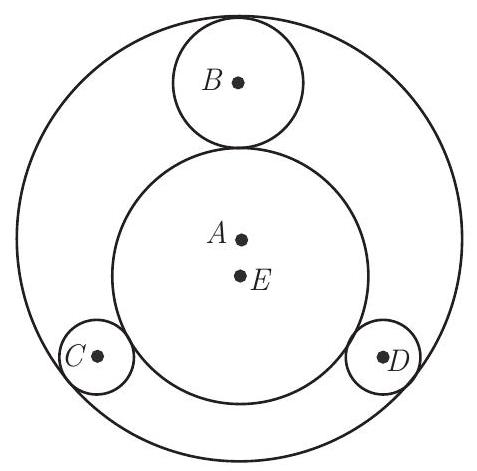
Solution:
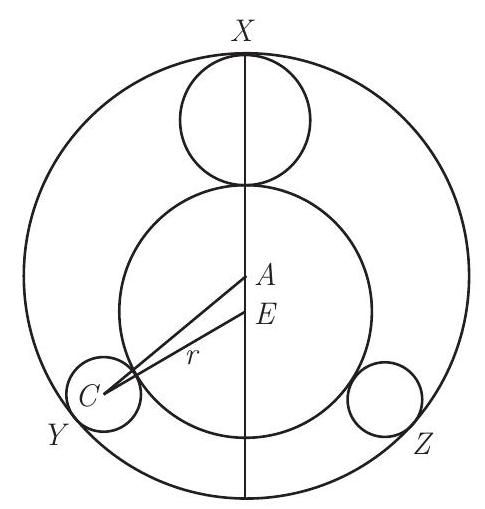
Let circles , and be tangent to circle at points , and , respectively. Circle has radius . Because circles and are congruent, point is on the diameter of circle through point . Note that , , and . Therefore by the Law of Cosines, it follows that . Expanding and simplifying yields . Solving for gives . The requested answer is .
The problems on this page are the property of the MAA's American Mathematics Competitions