Problem:
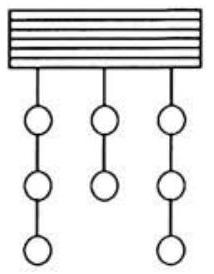
In a shooting match, eight clay targets are arranged in two hanging columns of three each and one column of two, as pictured. A marksman is to break all eight targets according to the following rules:
The marksman first chooses a column from which a target is to be broken.
The marksman must then break the lowest remaining unbroken target in the chosen column. If these rules are followed, in how many different orders can the eight targets be broken?
Solution:
Consider the eight shots that must be fired to break the eight targets. Of the eight, any subset of three shots may be the shots used to break the targets in the first column (but once these three shots are chosen the rules of the match determine the order in which the targets in the first column will be broken by these shots.) This set of shots for the first column may be chosen in ways. From the remaining five shots, the three used to break the targets in the other column of three may be chosen in ways, while the remaining two shots will be used to break the remaining two targets. Combining, we find that the number of orders in which the targets can be broken is
The problems on this page are the property of the MAA's American Mathematics Competitions