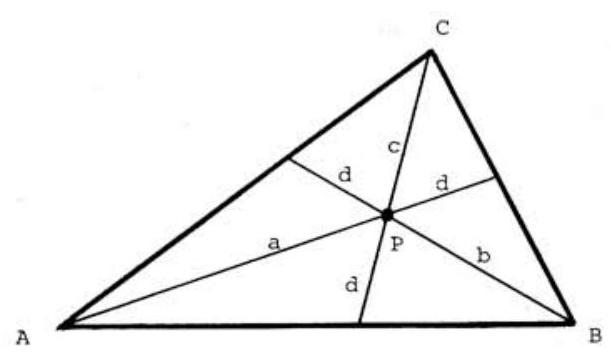
Problem:
Let P be an interior point of â–³ABC and extend lines from the vertices through P to the opposite sides. Let a,b,c, and d denote the lengths of the segments indicated in the figure. Find the product abc if a+b+c=43 and d=3.
Solution:
First observe that
d+ad​=area(△BAC)area(△BPC)​,(1)
d+bd​=area(△CBA)area(△CPA)​(2)
d+cd​=area(△ACB)area(△APB)​(3)
Then, since area(â–³BPC)+area(â–³CPA)+area(â–³APB)=area(â–³ABC), the sum of (1), (2) and (3) simplifies to
d+ad​+d+bd​+d+cd​=1
Multiplying through by (d+a)(d+b)(d+c), expanding and grouping like terms, we may write the above as
2d3+(a+b+c)d2−abc=0(4)
From (4), in view of the given data it follows that abc=2⋅33+43⋅32=441​.
Note. One such triangle has a=b=21 and c=1. Show that there are infinitely many noncongruent triangles meeting the conditions of the problem. Is it true that if two of the quantities a+b+c,abc,d are given, then the third is uniquely determined and can be realized geometrically?
The problems on this page are the property of the MAA's American Mathematics Competitions
