Problem:
Let be an equiangular hexagon such that 10 , and . Denote by the diameter of the largest circle that fits inside the hexagon. Find .
Solution:
Because each interior angle of an equiangular hexagon is , attaching two equilateral triangles to two opposite sides of the hexagon gives a parallelogram with and angles as shown in the diagram.
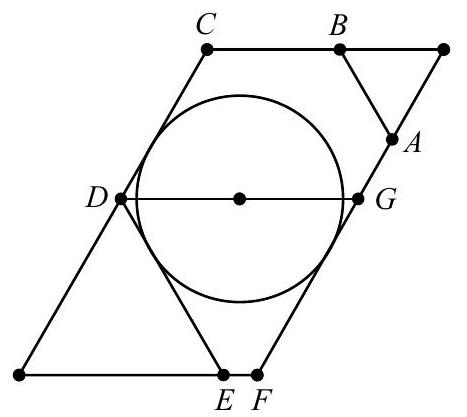
The fact that the opposite sides in the parallelogram must be congruent implies that the sum of the lengths of any two adjacent sides of the hexagon is the same as the sum of the lengths of the two opposite sides. From it follows that , and from it follows that .
The fact that the parallelogram has angles implies that the distance between two opposite parallel sides of the hexagon is times the sum of the lengths of the two adjacent sides connecting them. The shortest distance between the
parallelogram's opposite sides is thus the distance from line to line , which is . Let lie on so that . Because is the bisector of , the midpoint of is from each of the lines , and . Its distance from line is , its distance from line is , and its distance from line is . This shows that the midpoint of is the center of a circle with diameter that fits inside the hexagon, and no larger circle will fit between and . The requested square of this diameter is .
The problems on this page are the property of the MAA's American Mathematics Competitions