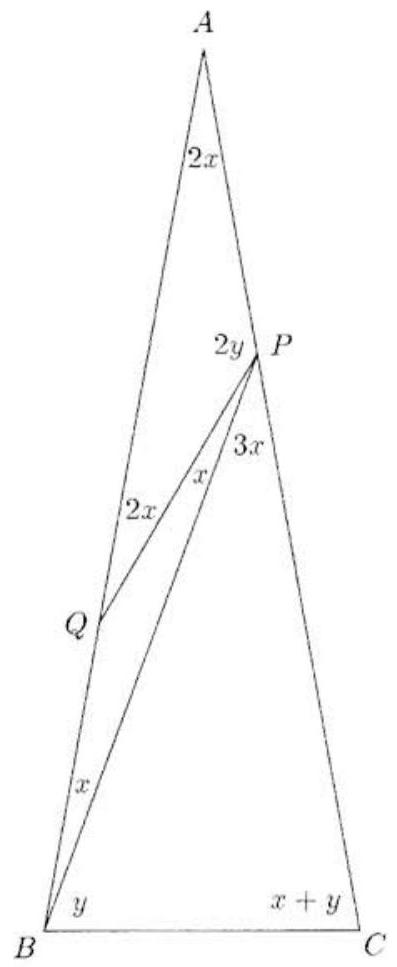
Problem:
In triangle ABC, it is given that angles B and C are congruent. Points P and Q lie on AC and AB, respectively, so that AP=PQ=QB=BC. Angle ACB is r times as large as angle APQ, where r is a positive real number. Find the greatest integer that does not exceed 1000r.
Solution:
Let x denote the degree measure of angle QPB. Because angle AQP is exterior to isosceles triangle BQP. its measure is 2x, and angle PAQ has the same measure. Because angle BPC is exterior to triangle BPA, its measure is 3x. Let y denote the measure of angle PBC. It follows that the measure of angle ACB is x+y, and that 4x+2y=180. Two of the angles of triangle APQ have measure 2x, and thus the measure of angle APQ is 2y. It follows that AQ=2⋅AP⋅siny. Because AB=AC and AP=QB, it also follows that AQ=PC. Now apply the Law of Sines to triangle PBC to find that
BCsin3x=PCsiny=2⋅AP⋅sinysiny=2⋅BC1
because AP=BC. Hence sin3x=21. This and 4x<180 imply that 3x=30 and x=10. Thus y=70 and r=2⋅7010+70=74, so 1000r=571+73.
OR
Let u=∠ACB=∠ABC. Then ∠A=∠AQP=180−2u,∠APQ=4u−180,∠QBP= ∠QPB=90−u,∠BQC=∠BCQ=90−21u,∠CQP=25u−90, and ∠QCP=23u−90. Apply the Law of Sines to triangles △PQ and CPQ to obtain
sin(180−2u)sin(4u−180)=APAQ=PQPC=sin(23u−90)sin(25u−90)
This is equivalent to
sin2u−sin4u=cos23ucos25u
or −2cos2ucos23u=cos25u. Use the identity 2cosαcosβ=cos(α−β)+cos(α+β) to obtain cos27u+cos25u+cos21u=0, and then again to obtain 2cos3ucos21u+cos21u=0. This implies that cos3u=−21. so that u=40 or u=80. Because 4u must be greater than 180 , it follows that u=80. Thus ∠APQ=4u−180=140 and r=4/7, as above.
The problems on this page are the property of the MAA's American Mathematics Competitions