Problem:
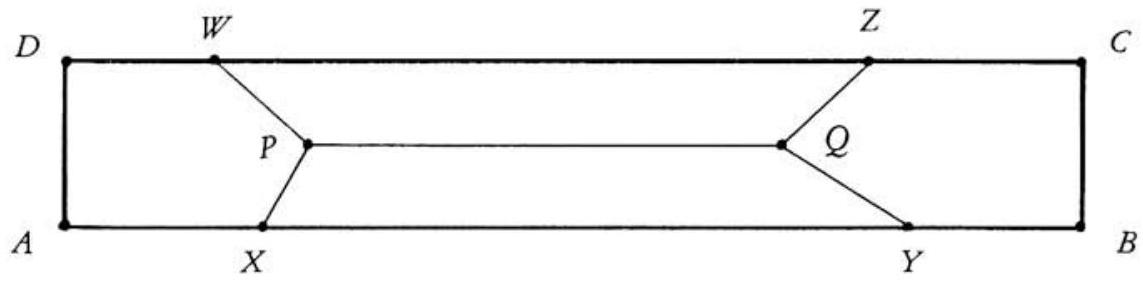
Rectangle ABCD is divided into four parts of equal area by five segments as shown in the figure, where XY=YB+BC+CZ=ZW=WD+DA+AX, and PQ is parallel to AB. Find the length of AB (in cm) if BC=19 cm and PQ=87 cm.
Solution:
Since trapezoids XYQP and ZWPQ have the same area, and since their parallel sides are of the same length, their heights must also be equal, each of length BC/2. Moreover, since XY is one fourth of the perimeter of rectangle ABCD, it follows that XY=2(AB+BC), and that the area of trapezoid XYQP is 2PQ+[(AB+BC)/2]⋅2BC. Since this must be equal to one fourth of the area of rectangle ABCD, one finds that
2PQ+[(AB+BC)/2]⋅2BC=4AB⋅BC,
from which AB=BC+2⋅PQ=19+2⋅87=193 cm.
The problems on this page are the property of the MAA's American Mathematics Competitions