Problem:
The eyelets for the lace of a sneaker all lie on a rectangle, four equally spaced on each of the longer sides. The rectangle has a width of and a length of . There is one eyelet at each vertex of the rectangle. The lace itself must pass between the vertex eyelets along a width side of the rectangle and then crisscross between successive eyelets until it reaches the two eyelets at the other width side of the rectangle as shown. After passing through these final eyelets, each of the ends of the lace must extend at least farther to allow a knot to be tied. Find the minimum length of the lace in millimeters.
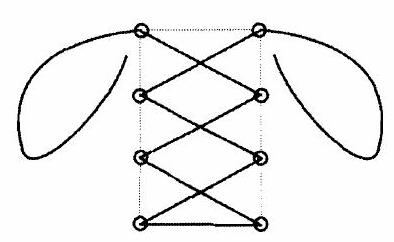
Solution:
The lace must be long enough to pass along one width of the rectangle and six diagonal crisscrosses, and include the two loose ends for tying the knot. The width is . The diagonals are hypotenuses of right triangles with legs measuring and . Because , these numbers are proportional to the first two terms of the Pythagorean triple and the diagonal length is . The total length required is therefore .
The problems on this page are the property of the MAA's American Mathematics Competitions