Problem:
Let be the set of points in the Cartesian plane that satisfy
If a model of were built from wire of negligible thickness, then the total length of wire required would be , where and are positive integers and is not divisible by the square of any prime number. Find .
Solution:
Making use of symmetry, graph the part in the first quadrant and then reflect this in the coordinate axes. In the first quadrant, the defining equation simplifies to
Again making use of symmetry, graph the part in the region and then reflect this in the lines and . In this region, the equation simplifies further to
the graph of which is a square, whose vertices are , and , and whose perimeter is .
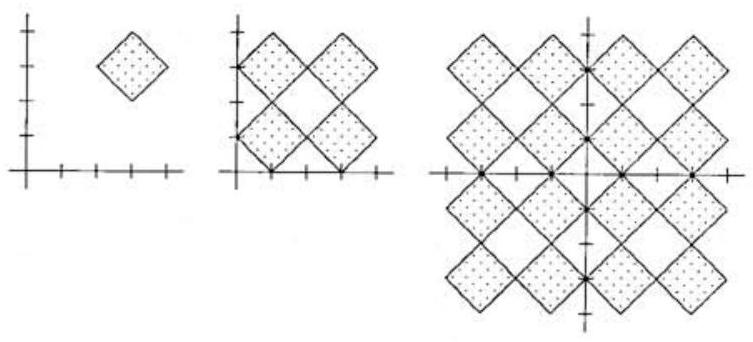
Reflection in the line and then in the line produces a set of squares for which the required length of wire is , as shown in the middle figure. Reflection in the coordinate axes then produces a set of squares for which the required length of wire is , as shown in the third figure. Thus .
The problems on this page are the property of the MAA's American Mathematics Competitions