Problem:
For all positive integers , let
and define a sequence as follows: and for all positive integers . Let be the smallest such that . (For example, 3 and .) Let be the number of positive integers such that . Find the sum of the distinct prime factors of .
Solution:
For , let denote the set of positive integers such that . Then, for example, , and . This can be illustrated in a tree diagram, as shown.
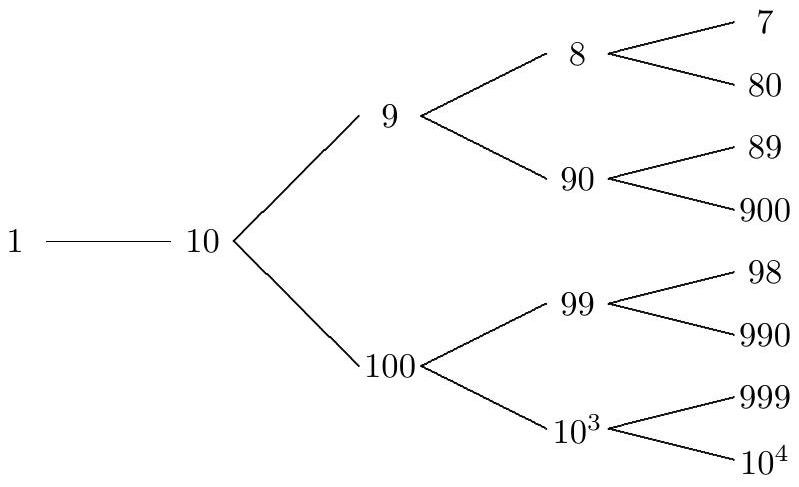
If each vertex in this tree after the first column had two branches, then the th column would have vertices; but some vertices have only one branch, namely, the vertex that corresponds to and vertices that correspond to numbers with last digit . The vertex that corresponds to is in the th column. This causes there to be fewer vertices in the th column than there would be if each vertex in the tree had two branches. Note that vertices that correspond to numbers with last digit occur columns after vertices that correspond to numbers with last digit , except for . Thus there will be one in column , two 's in column , and in general, 's in column , for . For each of these eight columns, this causes there to be fewer vertices in the th column than there would be if each vertex in the tree had two branches. Thus is the number of elements in , that is, the number of vertices in column , namely,
and the sum of the distinct prime factors of is .
The problems on this page are the property of the MAA's American Mathematics Competitions