Problem:
Triangle ABC is isosceles with AC=BC and ∠ACB=106∘. Point M is in the interior of the triangle so that ∠MAC=7∘ and ∠MCA=23∘. Find the number of degrees in ∠CMB.
Solution:
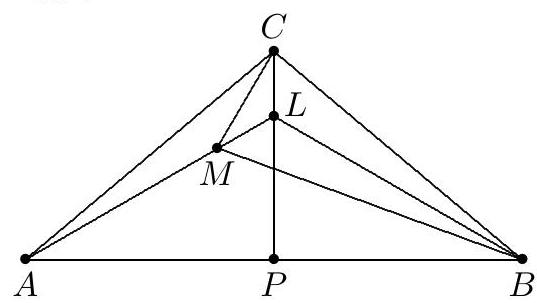
Let CP be the altitude to side AB. Extend AM to meet CP at point L, as shown. Since ∠ACL=53∘, conclude that ∠MCL=30∘. Also, ∠LMC= ∠MAC+∠ACM=30∘. Thus △MLC is isosceles with LM=LC and ∠MLC= 120∘. Because L is on the perpendicular bisector of AB,∠LBA=∠LAB=30∘ and ∠MLB=120∘. It follows that ∠BLC=120∘. Now consider △BLM and △BLC. They share BL,ML=LC, and ∠MLB=∠CLB=120∘. Therefore they are congruent, and ∠LMB=∠LCB=53∘. Hence ∠CMB=∠CML+ ∠LMB=30∘+53∘=83∘.
OR
Without loss of generality, assume that AC=BC=1. Apply the Law of Sines in △AMC to obtain
1sin150∘=CMsin7∘
from which CM=2sin7∘. Apply the Law of Cosines in △BMC to obtain MB2=4sin27∘+1−2⋅2sin7∘⋅cos83∘=4sin27∘+1−4sin27∘=1. Thus CB=MB, and ∠CMB=83∘.
The problems on this page are the property of the MAA's American Mathematics Competitions
