Problem:
A circle with diameter of length is internally tangent at to a circle of radius . Square is constructed with and on the larger circle, tangent at to the smaller circle, and the smaller circle outside . The length of can be written in the form , where and are integers. Find .
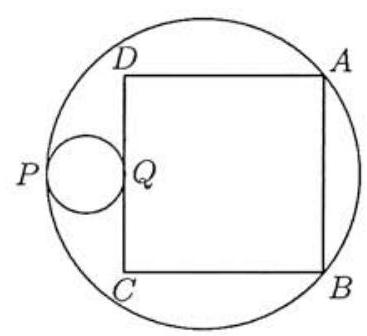
Solution:
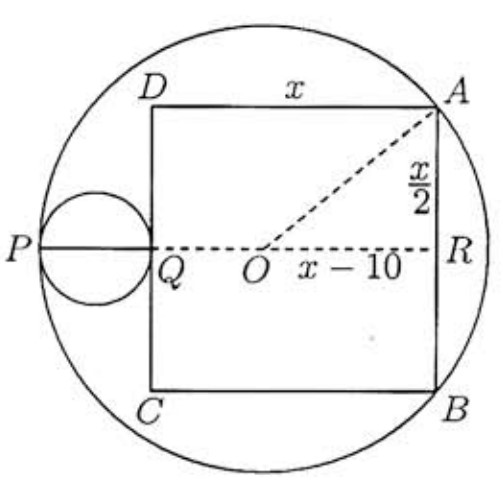
Let be the center of the large circle. Note that , and are collinear since the circles are tangent. Let the line through , and intersect in and let . Then . Because is tangent at to the smaller circle, it follows that and that is a right angle. Hence, by the Pythagorean Theorem,
Solving for , we obtain . Since , we have , and .
The problems on this page are the property of the MAA's American Mathematics Competitions