Problem:
Consider the region A in the complex plane that consists of all points z such that both z/40 and 40/zˉ have real and imaginary parts between 0 and 1 inclusive. What is the integer that is nearest the area of A? (If z=x+iy with x and y real, then zˉ=x−iy is the conjugate of z.)
Solution:
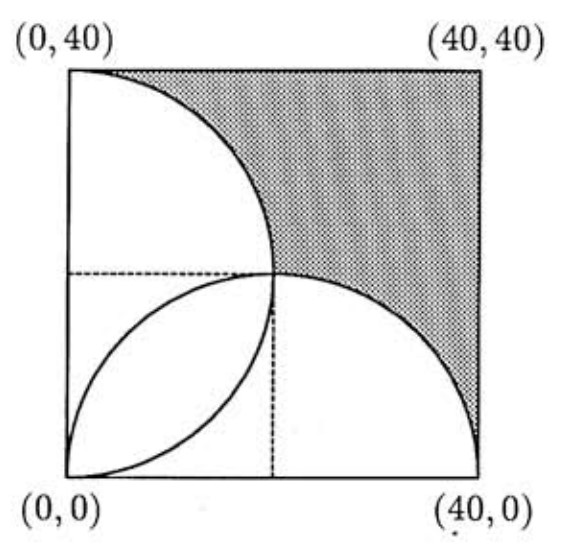
Let z=x+iy. For z to be in the region in question, we must have 0≤x≤40 and 0≤y≤40. Hence the region lies in the square with vertices (0,0),(40,0),(40,40), and (0,40). Next note that
zˉ40=x−iy40=x2+y240x+ix2+y240y
Hence the restrictions on the real and imaginary parts of zˉ40 give
0≤x2+y240x≤1 and 0≤x2+y240y≤1
from which
(x−20)2+y2≥202 and x2+(y−20)2≥202.
Thus the region in question lies outside the circle with center (20,0) and radius 20 and also outside the circle with center (0,20) and radius 20, as indicated by the shaded portion of the diagram. As suggested by the dashed lines in the diagram, the area of the region is 43 the area of the square minus the area of two quarter-circles. Hence
Area(A)=43⋅402−42(π⋅202)=200(6−π)≈571.7
so that the desired number is 572.
The problems on this page are the property of the MAA's American Mathematics Competitions