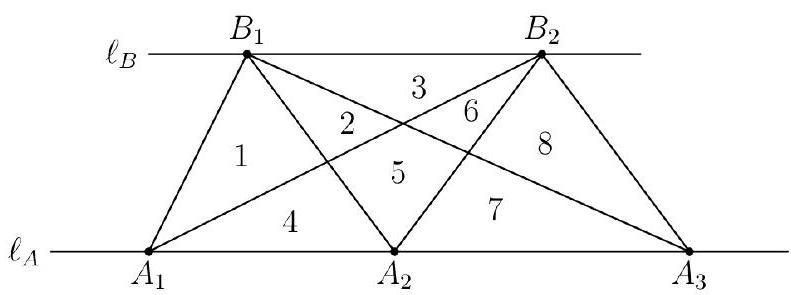
Problem:
Let ℓA and ℓB be two distinct parallel lines. For positive integers m and n, distinct points A1,A2,A3,…,Am lie on ℓA, and distinct points B1,B2,B3,…,Bn lie on ℓB. Additionally, when segments AiBj are drawn for all i=1,2,3,…,m and j=1,2,3,…,n, no point strictly between ℓA and ℓB lies on more than 1 of the segments. Find the number of bounded regions into which this figure divides the plane when m=7 and n=5. The figure shows that there are 8 regions when m=3 and n=2
Solution:
Assume that the points A1,A2,A3,…,Am and B1,B2,B3,…,Bn lie in these orders on the lines ℓA and ℓB, respectively, so that ℓA and ℓB together with the segments A1B1 and AmBn bound one region in the plane. Consider adding the other line segments AiBj one at a time. One of these line segments divides each of k regions into two regions where k−1 is the number of times AiBj intersects another of these line segments at a point between ℓA and ℓB. It follows that the final number of regions must be 1 plus 2 less than the number of line segments drawn plus the number of intersection points of these segments between ℓA and ℓB. Because there is one intersection point for every set of 4 points {Ap,Aq,Br,Bs} with 1≤p<q≤m and 1≤r<s≤n, the total number of regions is
1+(m⋅n−2)+(2m)(2n)
Substituting m=7 and n=5 gives
1+(7⋅5−2)+(27)(25)=244
OR
For a fixed value of m≥2, let f(n) be the number of bounded regions for given values of n. Then f(1)=m−1. To obtain f(n) from f(n−1), notice that adding the segment AiBn creates 1+(m−i)(n−1) new regions, so adding Bn to ℓB creates
1+[1+(n−1)]+[1+2(n−1)]+⋯+[1+(m−1)(n−1)]=m+2(n−1)m(m−1)
new regions as segments from the new point to the points on ℓA are drawn. Therefore
f(n)=f(n−1)+m+2(n−1)m(m−1).
Computing recursively when m=7 gives f(1)=6,f(2)=34,f(3)=83,f(4)=153, and f(5)=244, which is the requested number of regions.
\section*{OR}
Consider the graph whose vertices are A1,A2,A3,…,Am,B1,B2,B3,…,Bn, and the intersections of the AiBj line segments, and whose edges follow the AiBj,B1Bn, or A1Am line segments. Then this graph has m vertices on line ℓA,n vertices on line ℓB, and p=(2m)(2n) vertices between the two lines for a total of m+n+p vertices. Vertices A1 and Am each have degree n+1, and each vertex Ai for 1<i<n has degree n+2. Similarly, vertices B1 and Bn each have degree m+1, and each vertex Bj for 1<j<n has degree m+2. Each vertex between lines ℓA and ℓB has degree 4 . Thus the total of all the degrees of the vertices in the graph is
m(n+2)−2+n(m+2)−2+4p=2(mn+m+n−2+2p)
Hence the number of edges in the graph is half of this number which is mn+m+n−2+2p.\
Euler's Formula gives the number of bounded regions for a planar graph as 1 more than the number of edges minus the number of vertices, which, in this case, is
(mn+m+n−2+2p)−(m+n+p)+1=mn+p−1
When m=7 and n=5, this equals 7⋅5+(27)(25)−1=244.
The problems on this page are the property of the MAA's American Mathematics Competitions